端末座標系を世界座標系に

出席率

• 3年セミナー：??%

スケジュール

短期的な予定

• 端末座標系を世界座標系に
  • データをとる
  • 重力に対する各軸の傾きを出す
  • 2次元ベクトルを回転させる
  • 3次元ベクトルを回転させる
  • 端末座標系を世界座標系に変換する

長期的な予定

• 8/5 技育キャンプ ハッカソン
• 8/12 技育展
• 8/26 OpenHackU
• 9/2 技育キャンプ アドバンス
• 10/7,8 工科展

進捗報告

3次元ベクトルを回転させる

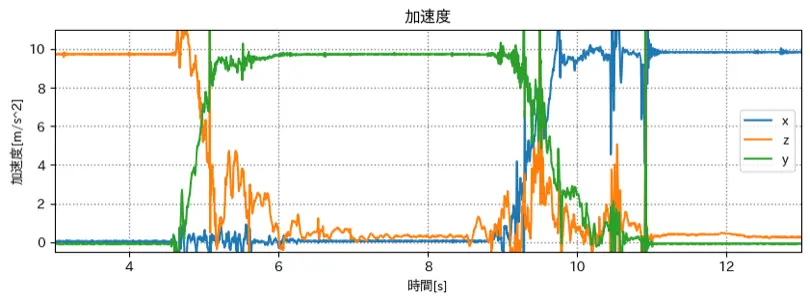
元の加速度

端末の傾き

元の加速度 を 端末の傾き だけ回転させる

回転後のベクトル

理想は y は常に9.8, x,z は常に0 になるはず
=> roll, pitch, yaw の回転のさせ方の問題？

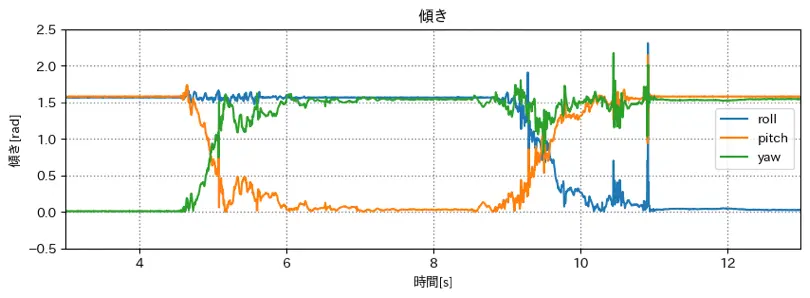
roll だけ掛けたグラフ

y(橙) が理想に近づいた

pitch だけ掛けたグラフ

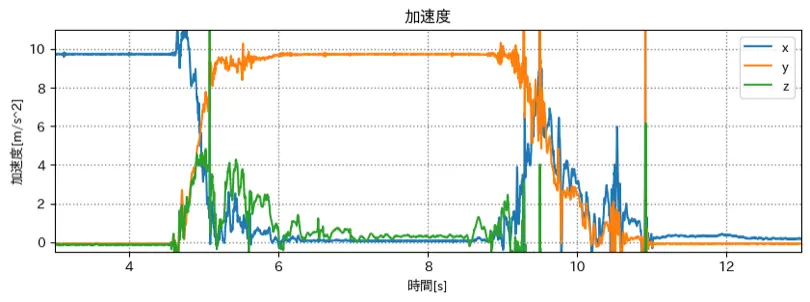
yaw だけ掛けたグラフ

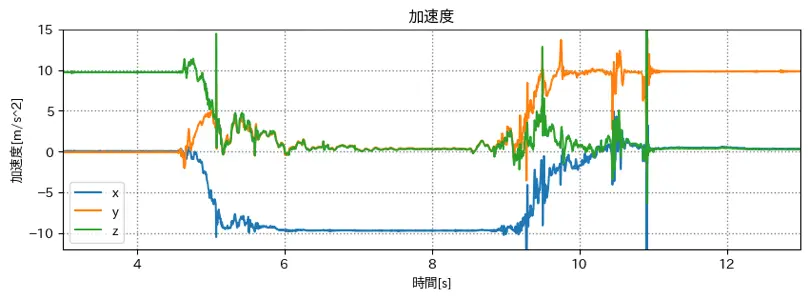
上下が合えばいいから roll, pitch, yaw 全て使う必要はないかも?

考え直す

計算した roll, pitch, yaw が入れ替わってしまっている可能性がある

端末の座標系

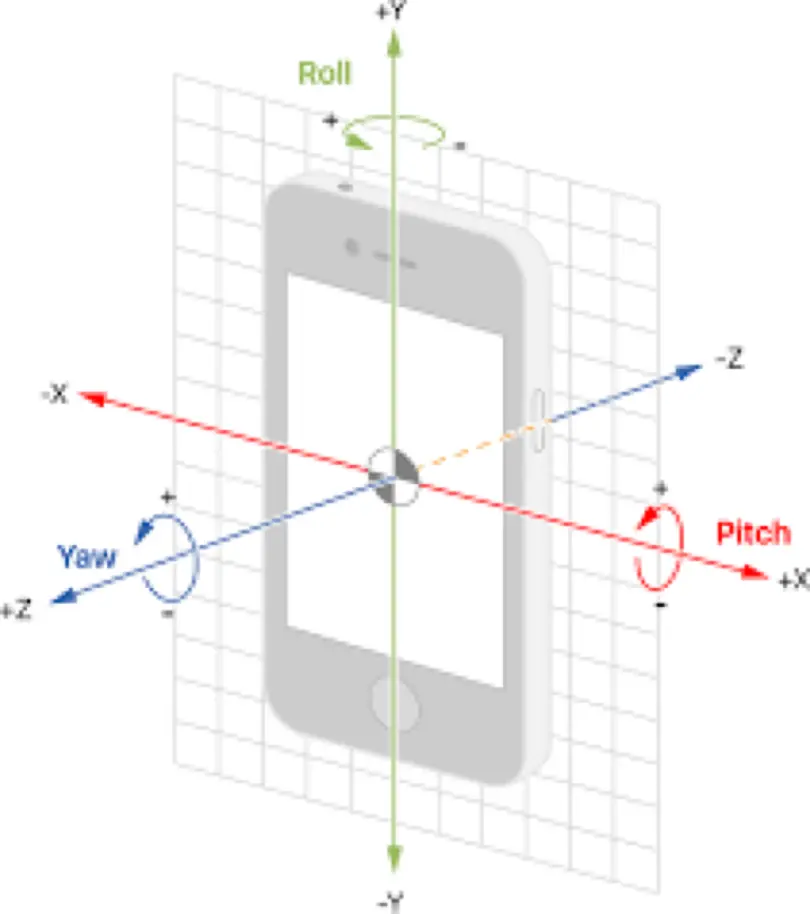
端末の傾き

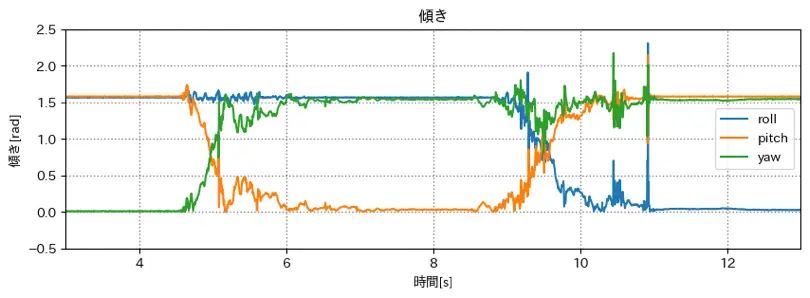
0s - 4s

端末の状態は z軸正が上向き
=> pitch 以外が回転している

傾きが 0deg である 緑 は pitch か yaw
(yaw として扱っていた)

6s - 8s

端末の状態は y軸正が上向き
=> 傾きが 0deg である 橙 が roll か pitch
(pitch として扱っていた)

11s - 13s

端末の状態は x軸正が上向き
=> 傾きが 0deg である 青 が roll か yaw
(roll として扱っていた)

変更後のグラフ 1

• roll: 橙
• yaw: 青
• pitch: 緑

とした場合のグラフ

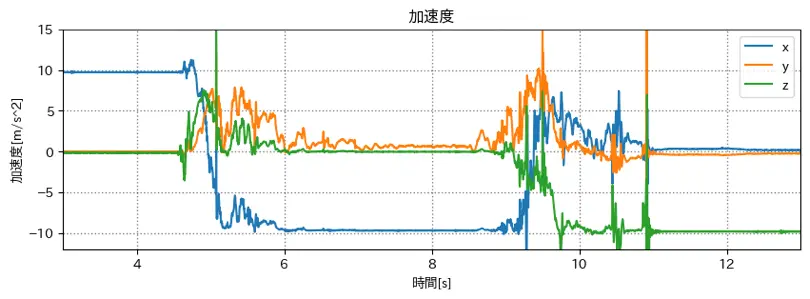
違う.

変更後のグラフ 2

いろいろ試してみた

• roll: 青
• yaw: 橙
• pitch: 緑

とした場合のグラフ

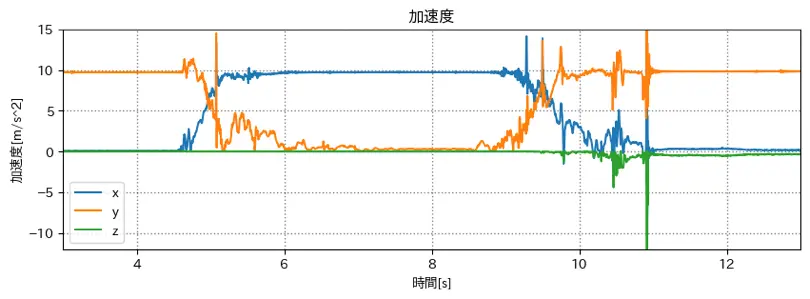
緑(z軸) が 常にほぼ 0(m/s^2) になった.
y軸が 9.8(m/s^2) になって欲しい

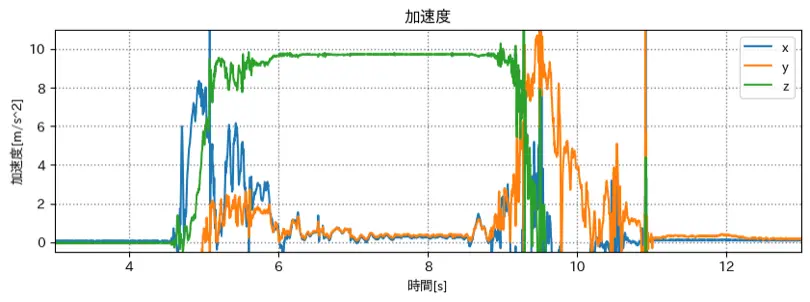
変更後のグラフ 3

いろいろ試してみた

• roll: 青
• yaw: 緑
• pitch: 橙

とした場合のグラフ

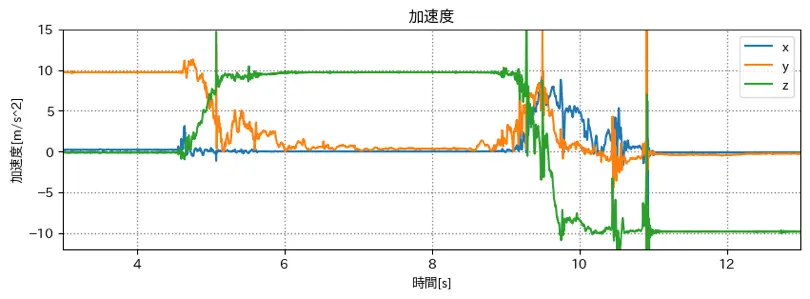
青(x軸) が 常にほぼ 0(m/s^2) になった.

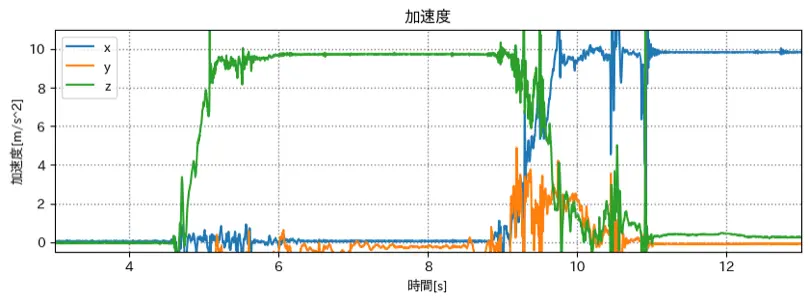
変更後のグラフ 4

いろいろ試してみた

• roll: 青
• yaw: 橙
• pitch: 緑

とした場合のグラフ

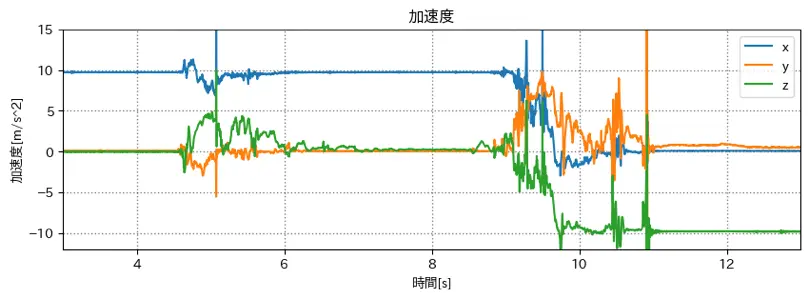
9秒までは結構理想的な形になっている.
ただし, 9.8(m/s^2) は x軸になっている.
(軸自体も間違っている可能性もある)

全パターン試したけど理想的な形のものにはならなかった.
x, z が 0 にはなるが y が 9.8 にならない.
=> 回転のさせ方が間違っている可能性がある

回転させる順番

回転させる順番によって結果変わってしまう.
3次元ベクトルを回転させる方法として正しくなさそう

回転行列

x軸周り

$$
R_x =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta \\
\end{bmatrix}
$$

y軸周り

$$
R_y =
\begin{bmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta \\
\end{bmatrix}
$$

z軸周り

$$
R_z =
\begin{bmatrix}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1 \
\end{bmatrix}
$$

としたとき,
回転行列をかける順番によって結果が変わる

$$
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
{\times}R_x
{\times}R_y
{\times}R_z
{\neq}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
{\times}R_y
{\times}R_x
{\times}R_z
$$

例

[2,3,5] のベクトルを全て 30deg回転させた結果

$$
\begin{bmatrix}
2.82 \\
4.25 \\
3.45 \\
\end{bmatrix} =
\begin{bmatrix}
2 \\
3 \\
5 \\
\end{bmatrix}
{\times}R_x
{\times}R_y
{\times}R_z
$$

$$
\begin{bmatrix}
0.83\\
5.24\\
3.12\\
\end{bmatrix} =
\begin{bmatrix}
2 \\
3 \\
5 \\
\end{bmatrix}
{\times}R_y
{\times}R_z
{\times}R_x
$$

余談

夏休み忙しそうだし、せっかくだからやめようと思った.
が, 店長がいい人すぎてお願いを断れなかった.
8-10月まで休みを貰うことに