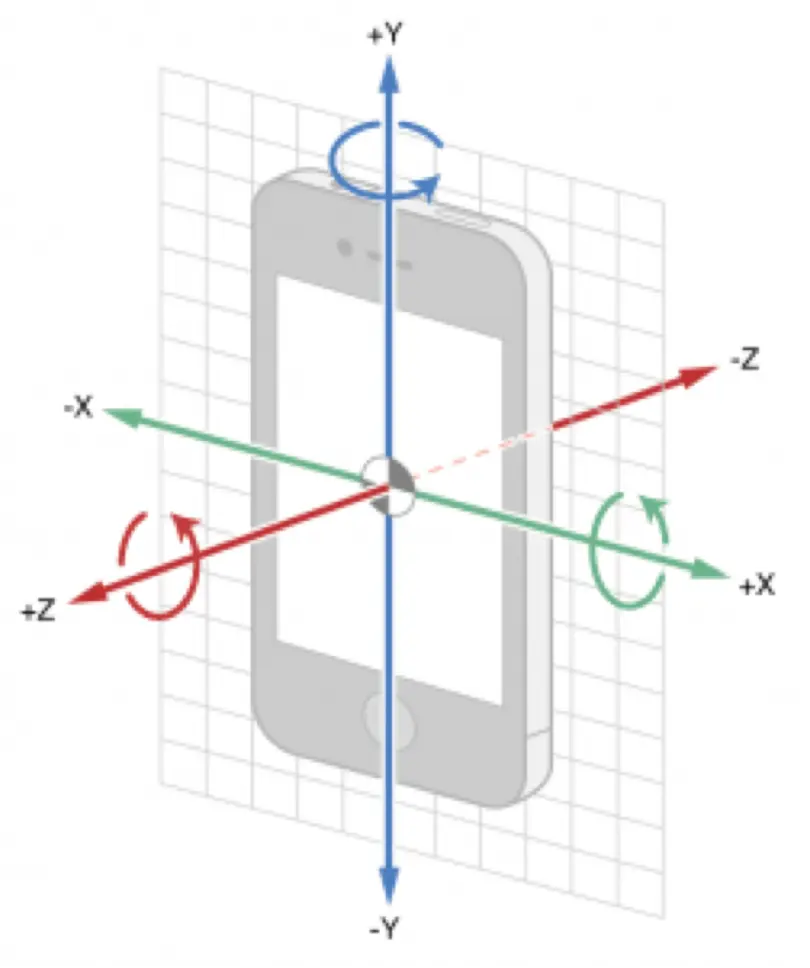
端末座標を世界座標に

出席率

• 3年セミナー：??%

スケジュール

短期的な予定

• 端末座標系を世界座標系に
  • データをとる
  • 重力に対する各軸の傾きを出す
  • 2次元ベクトルを回転させる
  • 3次元ベクトルを回転させる
• 技育キャンプ ハッカソン
  • テーマ決め
  • 開発練習
  • 7/9 キックオフ
  • 7/16 発表

長期的な予定

未定

進捗報告

方法

1. 各軸の加速度データから3次元ベクトルにする
2. 回転行列を掛けて回転させる
3. 3次元ベクトルから各軸の加速度にする

データをとる

• pixel5 (android)
• phyphox
  • 加速度センサー
  • 角速度センサー

1. z軸正が上(約4秒)
2. y軸正が上(約4秒)
3. x軸正が上(約4秒)

グラフ

加速度

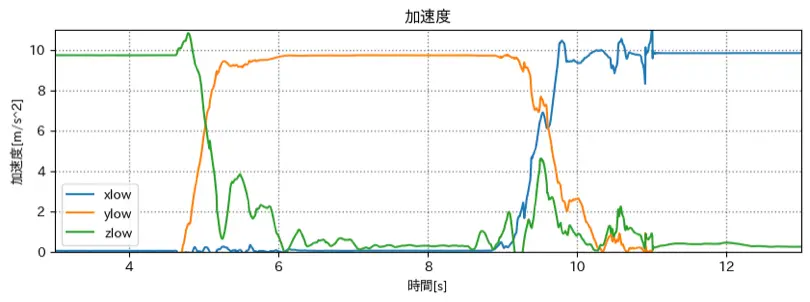
移動平均フィルター(前後40サンプル)をかけている

角速度

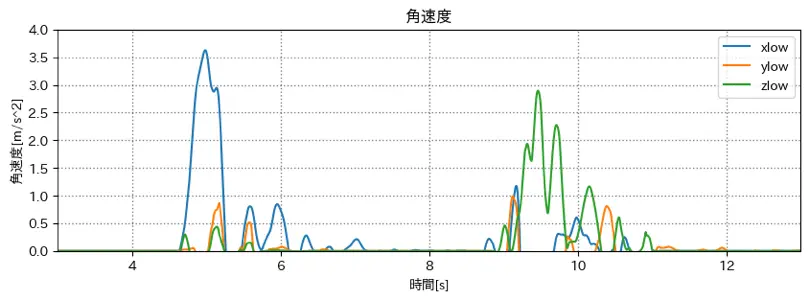
移動平均フィルター(前後40サンプル)をかけている

角度

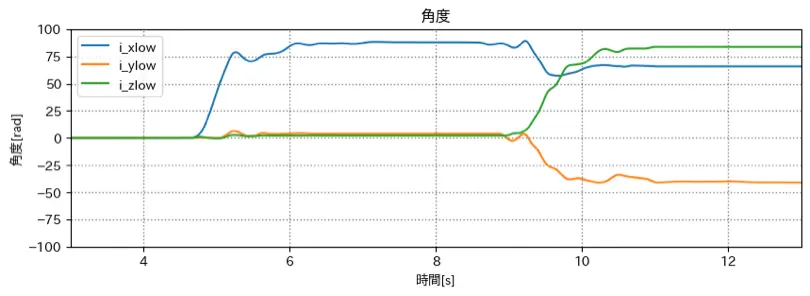
移動平均フィルターをかけたものを積分したもの

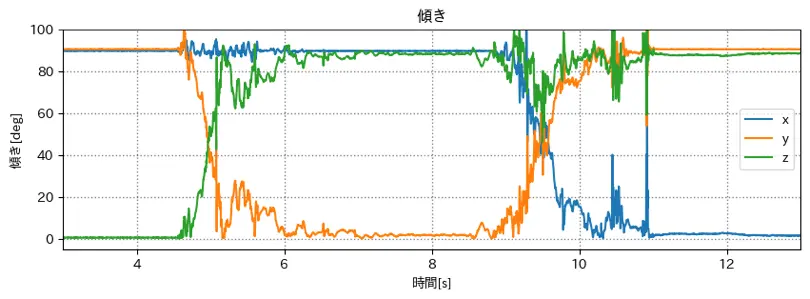
重力に対する各軸の傾きを出す

1gravity = math.sqrt(x ** 2 + y ** 2 + z ** 2)
2
3tilt_angle_x = math.degrees(math.acos(x / gravity))
4tilt_angle_y = math.degrees(math.acos(y / gravity))
5tilt_angle_z = math.degrees(math.acos(z / gravity))

重力に対するそれぞれの軸の傾き

ベクトルを回転させる方法

• 回転行列
• 外積の性質を利用
• クォータニオン

回転行列

回転行列はベクトルに対し始点を基準に回転させる
=> 始点は端末の中心とし、端末座標系を回転させれば世界座標系になるのでは

2次元ベクトルを回転させる

(いきなり3次元は無理があった)

計算方法(2次元)

θrad 回転する場合

$$
Vec^{\prime} =
\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
\end{bmatrix}
$$

Python

回転行列 R

1cos = np.cos(θ)
2sin = np.sin(θ)
3
4R = np.array(
5  [[cos, -sin], [sin, cos]]
6)

元のベクトル

1vec = [2, 0]

回転後のベクトル

1vec_dash = np.dot(R, vec)

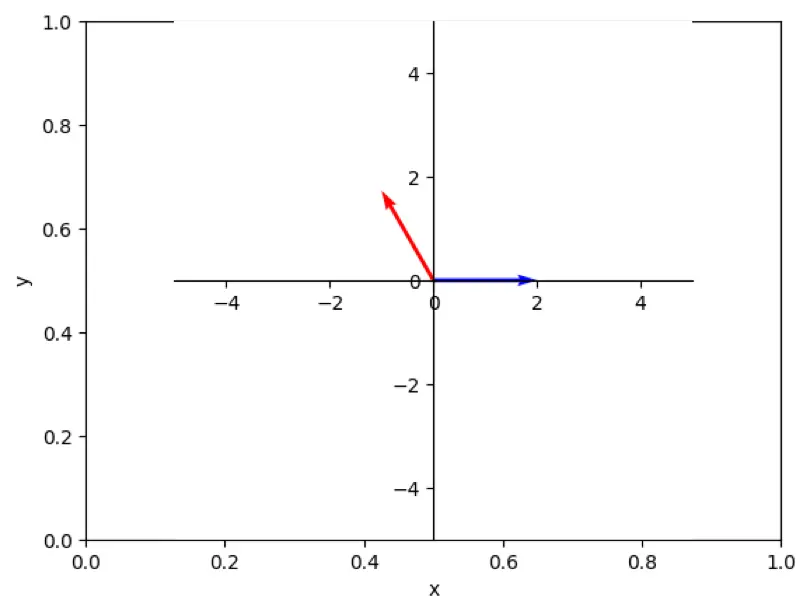
グラフ

青を 120deg 回転させた

3次元ベクトルを回転させる

計算方法(3次元)

θrad 回転する場合

x軸周り

$$
Vec_x^{\prime} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
$$

y軸周り

$$
Vec_y^{\prime} =
\begin{bmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
$$

z軸周り

$$
Vec_z^{\prime} =
\begin{bmatrix}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
$$

参考

• ベクトルの回転

余談

名刺作った!!